What is a Database Index? Why B+ Tree?

In backend development, developers frequently work with database indexes. That's why many companies ask the classic interview question: "What is a database index? What is indexing?" Understanding this concept is essential for writing efficient database queries and designing scalable systems.

In this article, we'll explore database indexes using SQL databases as our example. But before we answer the question, let's understand the problem indexes solve through a real scenario.

What Problems Occur Without Indexes?

Imagine you have a Products table, and users frequently search for products by price. Your SQL query might look like: SELECT * FROM Products WHERE Price BETWEEN 100 AND 200.

Without any special optimization, the database scans every single row and returns those matching the WHERE condition. This is like a linear search—the more data you have, the longer it takes to search through.

This O(n) approach means if you have 10,000 products, the database reads 10,000 rows. If you have a million products, it reads a million rows. As databases grow, this becomes increasingly inefficient.

Without special handling, the database scans linearly through every row. But what if we could make this more efficient? Just like books have indexes, we can add an index to our database.

I found a photo of a book index that perfectly illustrates this (it appears to be from a Japanese law exam study guide). Without an index, finding a specific legal term requires flipping through every page—just like our linear search. But with the index shown in the photo, you can jump directly to page 59.

Database indexes work similarly. When you create an index on a column, the database no longer needs to scan every row. Instead, it can quickly navigate to the relevant section and search there, making the entire process much faster.

What is an Index?

Now that you understand what problem indexes solve, let's formally answer: what is an index?

Just like a book's index is a separate page with its own structure (legal topics grouped together, for example), a database index is a data structure. This structure copies part of the original table's data and, using a sorted column, uses pointers to reference back to the original table. (Note: by using pointers, the index doesn't need to store all the data, reducing space requirements.)

When we create an index on the Price column in our Products table, the database creates an additional data structure:

CREATE INDEX idx_products_price ON Products(Price);

But what data structure should a database use to speed up searches?

When thinking about data structures that accelerate searching, many people first think of binary search trees. In a binary search tree, every node's key value is greater than all values in its left subtree and less than all values in its right subtree. In the example below, all values to the left of 50 are less than 50, and all values to the right are greater than 50.

        [50]
       /    \
    [30]    [70]
    /  \    /  \
  [20][40][60][80]

With this structure, searching becomes much faster. To find a value, you compare it with the root node. If it's larger, search the right subtree; if smaller, search the left subtree. By eliminating one half of the remaining data with each comparison, you're effectively cutting your search space in half.

With a million records, the first comparison eliminates 500,000 records, the second comparison eliminates 250,000, and so on—you only need about 20 comparisons to find your value. From a Big O perspective, linear scanning requires O(n) operations, but binary search tree navigation requires only O(log n).

For our Products table, after creating an index on the Price column using a binary search tree structure, we can use binary search to quickly find the target price, then use pointers to retrieve the corresponding data from the original table. This dramatically accelerates the entire search process.

While binary search trees work well for basic indexing, most relational databases don't actually use them. Instead, they use B-trees or B+ trees.

Why Choose B-tree or B+ Tree?

Before discussing B-trees, let's think about this: if we want to make binary search tree searches even faster, how could we improve?

We established that with a million records, a binary search tree reduces 20 comparisons from the linear scan. Could we reduce this number further? In 1971, computer scientists Rudolf Bayer and Edward M. McCreight introduced the B-tree, which effectively reduces the number of disk accesses needed.

The key characteristic of B-trees is that each node contains multiple keys, not just one. You can experiment with B-trees at https://btree.app/. With nodes containing up to 10 keys, constructing a B-tree for 1-100 requires three levels, needing only three reads. In contrast, a balanced binary search tree for 100 nodes requires at least seven levels.

With a million records, a binary search tree would have log₂(1,000,000) ≈ 20 levels. A B-tree with 100 keys per node would have log₁₀₀(1,000,000) ≈ 3 levels.

For database operations, comparing values with node keys is negligible. Comparing a value against 100 keys takes virtually the same time as comparing against 2. However, disk I/O operations (when data isn't cached) are expensive. If each disk read takes 10 milliseconds, reading 3 nodes versus 20 nodes saves 170 milliseconds.

B-trees allow each node to contain many keys. When controlled properly, this adds minimal overhead while dramatically reducing disk I/O. This makes B-trees far more efficient than binary search trees for database operations.

However, B-trees have efficiency problems in certain scenarios. For example, searching for a price range between 1000 and 2000 in a million-record database would require three disk reads for 1000, three for 1001, and so on—totaling 3000 disk reads (1000 × 3).

Since disk reads are one of the most time-consuming operations in database queries, consider this: could we further optimize B-tree design to reduce disk operations?

B+ trees, an improvement over B-trees, address this exact problem. You can visualize B+ trees at https://bplustree.app/. Look at the examples and compare B+ tree structure to the B-tree above.

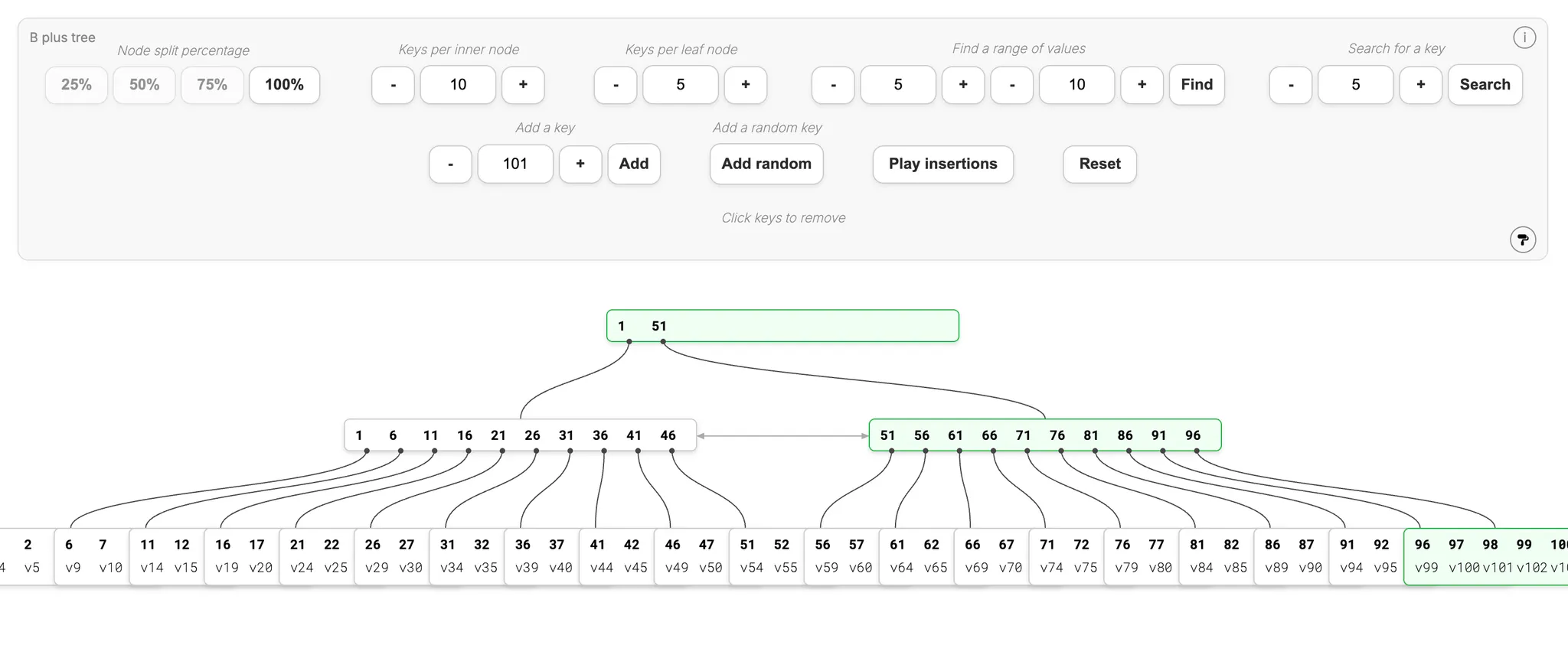
In the B+ tree above, values like 51 appear in multiple levels—the root node, intermediate nodes, and leaf nodes. In a B-tree, each value appears only once.

This design separates nodes into internal nodes and leaf nodes. Internal nodes act as pointers directing to leaf nodes, while actual data exists only in leaf nodes. Since internal nodes are easily cached and actual I/O happens at leaf nodes, this design significantly reduces disk reads and improves overall speed.

Additionally, since internal nodes only store keys and pointers (not actual records), they can store more keys in the same memory space, reducing tree height. Lower tree height means fewer disk reads needed, allowing the same queries to complete with fewer disk operations.