数据库索引 (Database Index) 是什么? 为什么用 B+ tree?

在后端开发的日常中，开发者经常会跟数据库索引 (database index) 打交道。也因此在后端的面试中，许多公司都很常会问「数据库的索引是什么? What is indexing?」这个问题。

在这篇文章中，我们会以 SQL 数据库为例，来讨论这个问题，不过在回答这个问题前，先让我们通过一个情境来了解，为什么需要索引?

没有索引会有什么问题?

假如今天有一张 Products 表，而用户经常会根据价钱来搜索产品，这时可能会写 SELECT * FROM Products WHERE Price BETWEEN 100 AND 200 这样的 SQL 语句。在没有特别做任何事情的情况下，数据库会扫过每一行，然后把符合 WHERE 条件的找出来。

这个概念就像线性搜索一样，当每多一条数据，未来搜索就会要多扫过一条数据。这种 O(n) 式的搜索，假如有一万条数据，就要扫过一万行，假如有百万条数据，就要扫过百万行。当数据库的数据多起来，拿数据会显得相对没有效率。

上面提到，没特别处理时，数据库会用线性的方式扫过每一行，这样很没有效率。如果要有效率一点，该怎么做呢? 相信这时你已经想到，就像我们在看书一样，可以加上索引。

这边找了一张 Google 「书本索引」出现的图 (看起来是日本某个司法考试准备的教科书的索引)，可以看到假如在没有索引的情况下，你要去找国税通则法，会需要一页页翻找，就像上面提到的线性搜索。然而，如果有了这个截图的索引，就可以直接跳到 59 页去找。

数据库的索引也是类似的概念，当你创建了某个列的索引，数据库在找数据时，就不再需用一行一行搜，而是可以更快速地到某个想搜的区域中，然后在该区域中搜索，让搜索的速度变快很多。

什么是索引?

在读完上面的段落，相信大家有理解索引是在解决什么问题。当你为数据库创建适当的索引，将能让你在做某些条件的搜索时，变得更快速。这时回到这个常见的面试题，什么是索引?

就像上面的日本司法考试教科书中的索引，是自己单独一页、有自己的结构 (例如民诉法放一起、民保法放一起)，索引是一种数据结构，这个数据结构会复制原表中的部分数据，然后依据排序好的列，通过指针指回原本的表 (备注：通过指针，在索引这个数据结构，就不用存所有的数据，所需的空间就能减少)。

因此，当我们为上面这个例子 (SELECT * FROM Products WHERE Price BETWEEN 100 AND 200) 所在的表中的 Price 列新增索引，数据库工具就会帮忙创建一个额外的数据结构。

CREATE INDEX idx_products_price ON Products(Price);

不过，在数据库中，该用什么样的数据结构来加速搜索呢?

相信提到能让搜索加速的数据结构，第一个会让人想到的是二元搜索树 (binary search tree)。在一棵二元搜索树中，每个节点的键值都大于左子树中所有节点的键值，且都小于其右子树中所有节点的键值。以下面的例子，50 的左子树的值都会是小于 50，而右子树中的所有值都大于 50。

        [50]
       /    \
    [30]    [70]
    /  \    /  \
  [20][40][60][80]

当数据结构这样设计，在搜索时就会快很多。假如要找到某个值，需要先与根节点比较；如果比根节点大，就往右子树找，如果比根节点小，就往左子树找。往其中一边的子树，就等于在搜索时，完全不用管另一边，等于面对的量就减半。

假如今天有百万条数据，第一次比较后就除去 50 万条，第二次比较再除去 25 万条，以此类推最多只要 20 次比较就能找到要找的值。从 Big O 的角度来看，原本扫过所有数据要 O(n)，但假如改成用二元搜索树的数据结构，能让搜索变 O(logn)。

以上面的 Products 表为例，当我们为 Price 创建索引后，假如用二元搜索树的结构来排序好 Price ，接着再用类似二元搜索 (binary search) 的树状搜索，让搜索时间复杂度大幅降低。找到要找的价格后，再用搭配的指针，指回原本表当中的相对应的数据，这样就能让整体的搜索加速许多。

上面我们谈了以二元搜索树作为索引的数据结构，来加速搜索。不过在实务上，多数关联数据库不是选用二元搜索树，而是用 B-tree 或 B+ tree 的数据结构。

为什么选用 B-tree 或 B+ Tree?

在谈 B-tree 之前，先让我们一起来思考，假如我们想让二元搜索树的搜索变更快，可以如何改善?

前面谈到，在有百万条数据的情况下，把数据结构设计成二元搜索树，就不需要扫过百万条，而是只要读取 20 次即可。有没有可能通过某些方法，让这个读取的次数再往下降? 在 1971 年时，两位电脑科学家 Rudolf Bayer and Edward M. McCreight 提出的 B-tree 就是一个能有效降低读取次数的结构。

具体来说，B-tree 的一大特点是每一个节点都不只有一个键，而是有多个键。在 https://btree.app/ 这个网站中，可以实际动手构建 B-tree。下面是以「每个节点最多到 10 个键」为例，假如构建一个 1 到 100 的 B-tree 会有三层，所以搜索最多只需要读取三次。但假如在一个平衡的二元搜索树，100 个数会要至少七层。

假如今天有百万条数据，用二元搜索树来呈现的话，因为每个节点有两个子节点，从数学上看 log₂(1000000)，所以会有 20 层。不过假如使用 B-tree，且每个节点如果有 100 个键，log₁₀₀(1000000) 则是会有 3 层。

对数据库读数据来说，在比较值与节点的大小，速度快到可以忽略不计。因此，假如每个节点有一百个键，要去比较某个值与键的值的大小，时间同样快到可以忽略。但在需要进行磁盘 I/O 的情况下 (例如没有命中快存时)，读取节点数据上，花的时间就无法忽略；假如读取每个节点要花 10 毫秒，读 3 个节点就会比读 20 个节点，少掉 170 毫秒。

因此，对数据库读取来说，B-tree 让每个节点带有比较多的键，假如控制在一定数量下，不会带来太多额外成本；同时，因为减少了读取磁盘的 I/O 所需时间，所以比起二元搜索树，是个让搜索能更快完成的数据结构。

不过 B-tree 的设计，在某些情境下仍然会有效率不高的问题。举例来说，假如要搜索一段范围，是上面的例子来说，假如在百万条数据中，要找价格在 1000 到 2000 之间的产品，在找价格 1000 的产品要读磁盘三次，找 1001 的产品也要读三次，一路到 2000 等于总共要读 3000 次 (1000 x 3)。

前面提到，在数据库查询数据时，最花时间的部分之一是在读磁盘中的数据这部分。推荐大家可以稍微暂停思考，在基于 B-tree 的数据结构下，有没有办法进一步调整，让读磁盘的动作变更少次?

B+ tree 这个基于 B-tree 改良的数据结构，就协助让读磁盘的操作变更少。在 https://bplustree.app/ 的网站中，能可视化地创建 B+ tree，以下是我们创建的范例，大家可以先观察一下 B+ tree 跟上面的 B-tree 在结构上有什么差别。

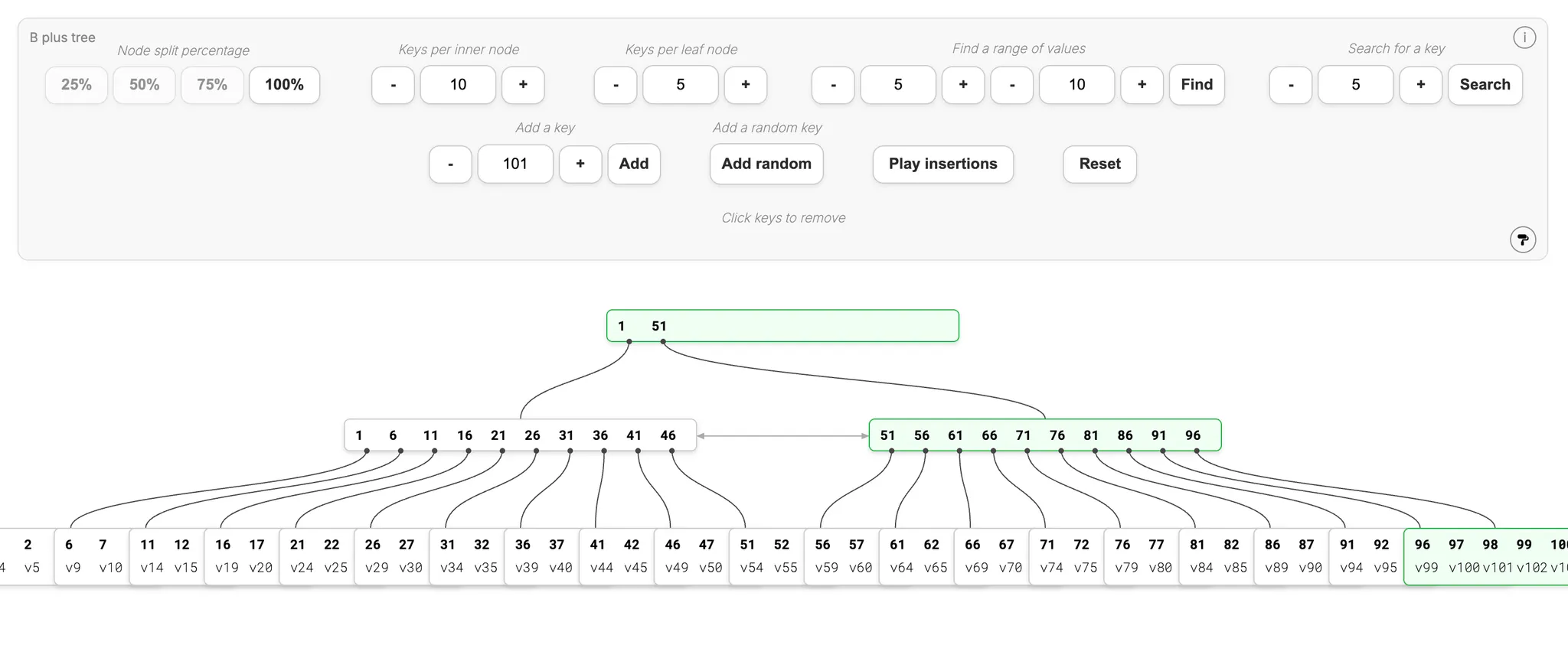
在上图中可以看到，在 B+ tree 当中，在最底下的子节点外的节点都有重复出现，以 51 为例，在根节点、第二层的节点，以及最底下的叶节点 (leaf node) 都有出现。对比之下，在 B-tree 的结构中，每个值只会出现在一个节点，不会这样重复出现。

这样的设计是因为 B+ tree 把节点分成内部节点 (internal nodes) 与叶节点 (leaf nodes)，内部节点只会作为指针 (pointer)，指向最终的叶节点，具体的值只会在叶节点。因为内部节点通常容易快存，实际发生大量 I/O 的地方是叶节点，当这样设计就能有效减少读取磁盘，让整体的速度更快。

除此之外，因为内部节点不存实际数据记录，只存键值和指针，可以在相同空间的记忆体中存更多键，降低整体的树高。如前面提到，树的高度下降，就意味着需要磁盘读取的次数会下降，用更少的磁盘读取次数，完成相同的查询。

没有索引会有什么问题?

什么是索引?

为什么选用 B-tree 或 B+ Tree?

阅读更多